Components of STAG 2.0
STAG 2.0 contains the following components:
Local Graph Clustering.
Given a vertex of some underlying graph as input, a local graph clustering algorithm is to find some low-conductance set around the input vertex, while the algorithm runs in time proportional to the size of the target cluster and independent of the size of the entire graph. As one of the key components in designing nearly-linear time graph algorithms, local graph clustering has been extensively studied in algorithmic spectral graph theory.
STAG contains our implemention of the local graph clustering based on PageRank (the ACL algorithm). Comparing with several existing open-source implementation for local graph clustering, our code connects to a Neo4j database running in the AuraDB cloud service, or a database running locally. With this feature, one can run local graph clustering on the entire Wikipedia graph of more than 20GB with a single PC.
A demo on local graph clusterin can be found here.

Reid Andersen, Fan R. K. Chung, Kevin J. Lang: Local Graph Partitioning using PageRank Vectors. FOCS 2006: 475-486
Daniel A. Spielman, Shang-Hua Teng: A Local Clustering Algorithm for Massive Graphs and Its Application to Nearly Linear Time Graph Partitioning. SIAM J. Comput. 42(1): 1-26 (2013)
Locality Sensitive Hashing.
Given a set of data points in a metric space, the goal of locality sensitive hashing is to preprocess the data in the way such that, given a new query point y, an algorithm is able to quickly recover the data points close to y.
STAG re-implements the previous C implemention by Andoni in order to take advantage of some modern features of C++.
Moses S Charikar. Similarity estimation techniques from rounding algorithms. In 34th Annual ACM Symposium on Theory of Computing (STOC’02), pages 380–388, 2002.
Mayur Datar, Nicole Immorlica, Piotr Indyk, and Vahab S Mirrokni. Locality-sensitive hashing scheme based on p-stable distributions. In Proceedings of the twentieth annual symposium on Computational geometry, pages 253–262, 2004.
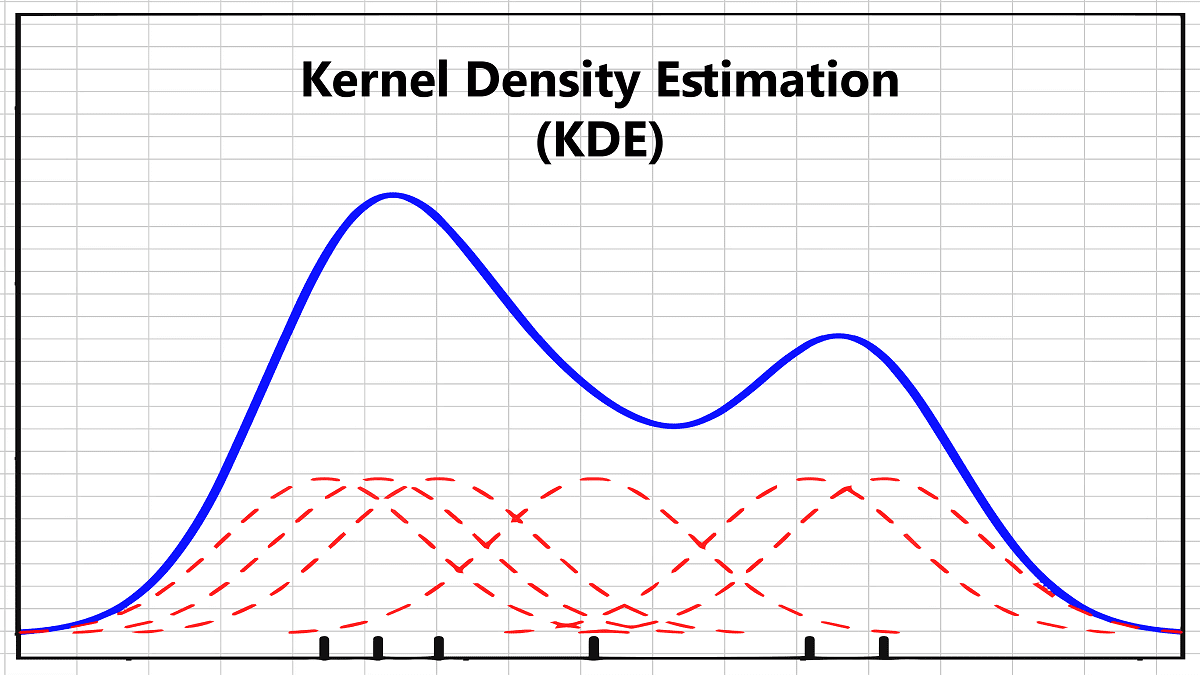
Kernel Density Estimation.
Kernel density estimation (KDE) is an important problem with many applications across machine learning and statistics. Given n data points and m query points, the goal of kernel density estimation is to fast approximate the sum of kernel functions between a query point and every data points. This problem can be seen as an estimate of the underlying probability density function from which the data is drawn and has been used for many applications in data science.
STAG contains our implemention of the CKNS algorithm for the Kernel Density Estimation problem.
Leslie Greengard and John Strain. The fast gauss transform. SIAM Journal on Scientific & Statistical Computing, 12(1):79–94, 1991.
Moses Charikar, Michael Kapralov, Navid Nouri, and Paris Siminelakis. Kernel density estimation through density constrained near neighbor search. In 61st Annual IEEE Symposium on Foundations of Computer Science (FOCS’20), pages 172–183, 2020.
Fast Spectral Clustering.
For any set of points in Euclidean space and parameter k, the goal of spectral clustering is to partition the points into k clusters such that similar points are grouped into the same cluster. It consists of the following three steps: (1) construct a similarity graph G; (2) compute the bottom k eigenvectors of the graph matrix, and apply these to embed the vertices into k-dim. space; (3) apply k-means on the embedded points, and use k-means’ output as the resulting clustering.
STAG contains the implementation of the fast spectral clustering algorithm designed by Macgregor and Sun. For data points from low dimension, their algorithm runs in nearly-linear time, and has theoretical guarantee on the output clusters.
Peter Macgregor and He Sun. Fast approximation of similarity graphs with kernel density estimation. Advances in Neural Information Processing Systems, 36, 2023.
Technical Reports
This series of technical reports is to document our progress on STAG, including implementation details, engineering considerations, and the data sets against which our implementation is tested.
Technical Report (1)
This report describes local graph clustering, provides a user guide to the essential features of STAG which allow a user to apply local clustering, and includes experiments and demonstrations of the functionality of STAG. The final part of the report discusses several technical details. Read here
Technical Report (2)
This report describes locality sensitive hashing, kernel density estimation, and fast spectral clustering. The report discusses the implemented algorithms, and experimentally compares our implementation with the others. The final part of the report discusses several technical details. Read here

About STAG

This project is part of He Sun's 5-year EPSRC Fellowship titled "Efficient Spectral Algorithms for Massive and Dynamic Graphs" with a total award of 1.5 million pounds. We are based in the School of Informatics, University of Edinburgh, United Kingdom.
Code
You can find STAG's source code from our Github page .
Funding Information
UK Engineering and Physical Sciences Research Council, EP/T00729X/1
Contact
Peter Macgregor
Research Associate
School of Informatics
University of Edinburgh
peter.macgregor@ed.ac.uk
Personal Webpage
He Sun
Reader
School of Informatics
University of Edinburgh
h.sun@ed.ac.uk
Personal Webpage
Postal address
School of Informatics
University of Edinburgh
Edinburgh, EH8 9AB
United Kingdom
